Začínáme počítat
Většina programátorů v Javě asi umí pracovat s čísly a dokáže si dobře spočítat, co by měl jejich program dělat. Jestli to potom opravdu dělá je věc druhá. Člověk si při učení Javy většinou začíná hrát s jednoduchými operátory (+ - * / %) a primitivními typy (int, double), po čase začne zkracovat (++ *= ...), sem tam použije bitové operace (| & ~ << >> >>>) a už se mu zdá, že je za vodou. Ale pak narazí na problémy.
Další level
Třeba taková nevinná konstrukce dělení. Žádné neukončené desetiné rozvoje nebo nedejbože dělení nulou.
double ctvrtina = 1 / 4; System.out.println(ctvrtina); //0.0 WTF?Stačí zapomenout, že výsledkem dělení celých čísel je opět celé číslo a máme oheň na střeše.
Další nástrahy se skrývají v číslech s plovoucí desetinou čárkou a s tím související nutností neustále zaokrouhlovat (např. když počítáte peníze na účtech pomocí typu double). Programátor si poté uvědomí, že třída BigDecimal je přesně to, co mu při počítání chybělo a že supertřída Number se dá využít na spoustu zajímavých věcí.
Na této úrovni už stojí za to hledat při řešení problémů různé zkratky a pomůcky.
Vyšší matematika – Apache commons Math

Asi nejznámější implementací dodatečných matematických úloh z různých oblastí je knihovna Math z projektu Apache Commons. Obsahuje funkce pro statistiku, lineární algebru, numerickou analýzu, odhad parametrů a další oblasti matematiky.
Logistická křivka – příklad použití estimatoru
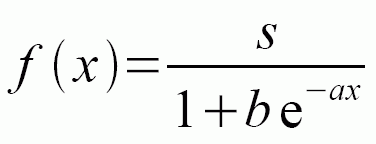
Nedávno jsem řešil výpočet logistické křivky a na tuto úlohu se hodí využít parametrický estimator z knihovny Math. Zdrojový kód vypadá takto:
/**
* Implementace vypoctu logisticke krivky (Wachstumskurve)
* s vyuzitim knihovny Math z Apache commons.
* <p>Logisticka krivka ma rovnici<br/>
* <code>f(x) = s / (1 + e^-z)</code><br/>
* Pro promennou <code>z</code> je pouzit linearni model, tedy<br/>
* <code>f(x) = s / (1 + b * e^(-a * x))</code>
* <code>s, a, b</code> jsou parametry modelu, ktere maji byt spocitany (odhadnuty).</p>
* <p>Trida LogisticProblem pouziva k reseni problemu nejmensich ctvercu
* Levenberg-Marquardt Estimator (pozor na licenci podminky).</p>
* @author Josef Cacek
*/
public class LogisticProblem extends SimpleEstimationProblem {
//Parametry logisticke funkce
private EstimatedParameter s;
private EstimatedParameter a;
private EstimatedParameter b;
//pomocne promenne
private double maxValue = 0d;
private boolean solved = false;
/**
* Pridava jednu namerenou hodnotu.
* @param aXValue
* @param aYValue namerena hodnota pro dane X
* @param aWeight vaha mereni
*/
public void addValue(double aXValue, double aYValue, double aWeight) {
double tmpXVal = recomputeXval(aXValue);
if (Math.abs(aYValue)>Math.abs(maxValue)) {
maxValue = aYValue;
}
addMeasurement(new LocalMeasurement(tmpXVal, aYValue, aWeight));
}
/**
* Vytvari Estimator a vypocita odhad. Vraci RMS.
* @return RMS (Root Mean Square value)
* @throws ProblemNotSolvedException kdyz se vyskytne problem pri estimaci
*/
public double solve() throws ProblemNotSolvedException {
if (solved) {
throw new IllegalStateException("Uz je to udelano, uz je to hotovo.");
}
solved = true;
if (getMeasurements().length<3) {
throw new ProblemNotSolvedException("Zadano prilis malo namerenych hodnot.");
}
//pridej parametry modelu a nastav pocatecni hodnoty pred iteraci
this.s = new EstimatedParameter("s", maxValue*2);
this.a = new EstimatedParameter("a", 1d);
this.b = new EstimatedParameter("b", 1d);
addParameter(this.s);
addParameter(this.a);
addParameter(this.b);
double RMS;
try {
// GaussNewtonEstimator estimator = new GaussNewtonEstimator(50, 1.0e-3, 1.0e-3);
LevenbergMarquardtEstimator estimator = new LevenbergMarquardtEstimator();
estimator.estimate(this);
RMS = estimator.getRMS(this);
} catch (EstimationException ee) {
ee.printStackTrace();
throw new ProblemNotSolvedException(ee);
}
return RMS;
}
/**
* Tato metoda muze implementovat prepocet hodnot na ose X. Napriklad, kdyz pracujeme
* s hodnotami, kde x znaci rok. je vhodne "posunout zacatek letopoctu". Napriklad,
* zacinaji-li namerene hodnoty rokem 2000, odecteme v teto funkci od X hodnotu 2000.
* @param aXval originalni hodnota na ose X
* @return prepocitana hodnota X
*/
private double recomputeXval(double aXval) {
//v nasem prikladu nemusime nic menit
return aXval;
}
/**
* Gets computed theoretical value for given timepoint.
* @param aTimeId
* @param aMaxPeriods
* @return
*/
public double getValue(double aXval) {
final double tmpXVal = recomputeXval(aXval);
return theoreticalValue(tmpXVal);
}
/**
* Estimated parameter S of logistic problem
* @return estimated parameter
*/
public double getS() {
return s.getEstimate();
}
/**
* Estimated parameter A of logistic problem
* @return estimated parameter
*/
public double getA() {
return a.getEstimate();
}
/**
* Estimated parameter B of logistic problem
* @return estimated parameter
*/
public double getB() {
return b.getEstimate();
}
/**
* Pocita teoretickou hodnotu pro dane X.
* @param aXval hodnota X
* @return vysledná hodnota funkce f(x)
*/
public double theoreticalValue(double aXval) {
// f(x, s, a, b)
return s.getEstimate() / (1d + b.getEstimate()*Math.exp(-a.getEstimate()*aXval));
}
/**
* Pocita hodnotu parcialnich derivaci pro dane x podle daneho parametru.
* @param aXval hodnota X
* @param aParam parametr, podle ktereho budeme derivovat
* @return hodnota parcialni derivace v x podle daneho parametru
*/
private double partial(double aXval, EstimatedParameter aParam) {
//tady nezbude programatorovi nic jineho nez oprasit znalosti matematicke
//analyzy a spocitat si parcialni derivace pozadovane funkce podle vsech
//pouzitych parametru
if (aParam == s) {
// Partial Derivative with respect to s
return 1d / (1d + b.getEstimate()*Math.exp(-a.getEstimate()*aXval));
} else if (aParam == a) {
// Partial Derivative with respect to a
return s.getEstimate()*b.getEstimate()*aXval*Math.exp(-a.getEstimate()*aXval)/
Math.pow(1d + b.getEstimate()*Math.exp(-a.getEstimate() * aXval), 2d);
} else {
// Partial Derivative with respect to b
return -s.getEstimate()*Math.exp(-a.getEstimate()*aXval)/
Math.pow(1d + b.getEstimate()*Math.exp(-a.getEstimate() * aXval), 2d);
}
}
/**
* Implementace namerenych hodnot - rozsiruje tridu WeightedMeasurement.
* Mereni je hodnota y pro dane vazane x.
*/
private class LocalMeasurement extends WeightedMeasurement {
private static final long serialVersionUID = 0L;
private final double x;
/**
* Constructor
* @param x measured X
* @param y measured Y
* @param w weighth
*/
public LocalMeasurement(double x, double y, double w) {
super(w, y);
this.x = x;
}
/**
* @see org.apache.commons.math.estimation.WeightedMeasurement#getTheoreticalValue()
*/
public double getTheoreticalValue() {
// the value is provided by the model for the local x
return theoreticalValue(x);
}
/**
* @see org.apache.commons.math.estimation.WeightedMeasurement#getPartial(org.apache.commons.math.estimation.EstimatedParameter)
*/
public double getPartial(EstimatedParameter parameter) {
// the value is provided by the model for the local x
return partial(x, parameter);
}
}
}
Jak už je poznamenáno ve zdrojovém kódu, je třeba dát si pozor na licenční podmínky u třídy LevenbergMarquardtEstimator a uvést příslušnou informaci v dokumentaci vašeho softwaru.
Použití této třídy může vypadat následovně:
package cz.cacek.logisticproblem;
import org.apache.commons.math.random.RandomData;
import org.apache.commons.math.random.RandomDataImpl;
/**
* Priklad pouziti generatoru nahodnych cisel z commons math
* a vypoctu logisticke krivky pro vygenerovanou nahodnou radu.
*
* @author Josef Cacek
*/
public class TestLogisticProblem {
/**
* Vypise na standardni vystup pole cisel
* @param aDesc popis hodnot
* @param aValues hodnoty k vypsani
*/
public static void printArray(String aDesc, double[] aValues) {
System.out.println("f(x) = " + aDesc + ":");
for (int i = 0; i < aValues.length; i++) {
System.out.print("f(" + i + ")=" + aValues[i] + ", ");
}
}
/**
* Vygeneruje ciselnou radu a resi logisticky problem pro tuto radu.
* @param args
*/
public static void main(String args[]) {
RandomData randomData = new RandomDataImpl();
double[] values = new double[15];
LogisticProblem lp = new LogisticProblem();
for (int i = 0; i < values.length; i++) {
values[i] = randomData.nextUniform(0d, 10000d);
lp.addValue(i, values[i], 1d);
}
printArray("Random values", values);
try {
double rms = lp.solve();
System.out.println("RMS = " + rms);
double[] lcValues = new double[15];
for (int i = 0; i < lcValues.length; i++) {
lcValues[i] = lp.theoreticalValue(i);
}
printArray("Logistic curve values", lcValues);
} catch (ProblemNotSolvedException e) {
//tady se nam muze stat napr toto:
//EstimationException: maximal number of evaluations exceeded (1,000)
e.printStackTrace();
}
}
}
Pro úplnost ještě třída s výjimkou, použitou v progamu:
package cz.cacek.logisticproblem;
/**
* Exception used for reporting problems during solving LogisticProblem
* (Wachstumskurve)
*
* @author Josef Cacek
*/
public class ProblemNotSolvedException extends Exception {
private static final long serialVersionUID = -81388704034021304L;
public ProblemNotSolvedException() {
}
public ProblemNotSolvedException(String message) {
super(message);
}
public ProblemNotSolvedException(Throwable cause) {
super(cause);
}
public ProblemNotSolvedException(String message, Throwable cause) {
super(message, cause);
}
}
Archiv se zdrojovými kódy příkladu si můžete stáhnout zde.
Komentáře
A pár malérů, které to způsobilo, už jsem taky viděl. :-)
double a = 0.9;
double b = 0.8;
double c = (0.9 - 0.8) * 10.0;
System.out.println((int) c); //vytiskne 0